LSTM简介
LSTM的全称叫Long Short Term Memory,即长短时记忆。它的主要优点就如名字中所说——可以同时记住长时间或短时间内的信息(或者说比较久远或者最近的信息)。网上也有很多相关的文章介绍LSTM,这里我们主要聚集几个方面:
- LSTM的网络结构有哪些特点?
- 这些特点可以带来哪些优势?
- LSTM的缺点有哪些?
LSTM的网络结构特点
LSTM是RNN的一种改进,它将RNN网络单元内的单一网络层修改为一种有着四种网络层的复杂结构。其总体结构如下(图片均来自台大李宏毅教授的PPT):
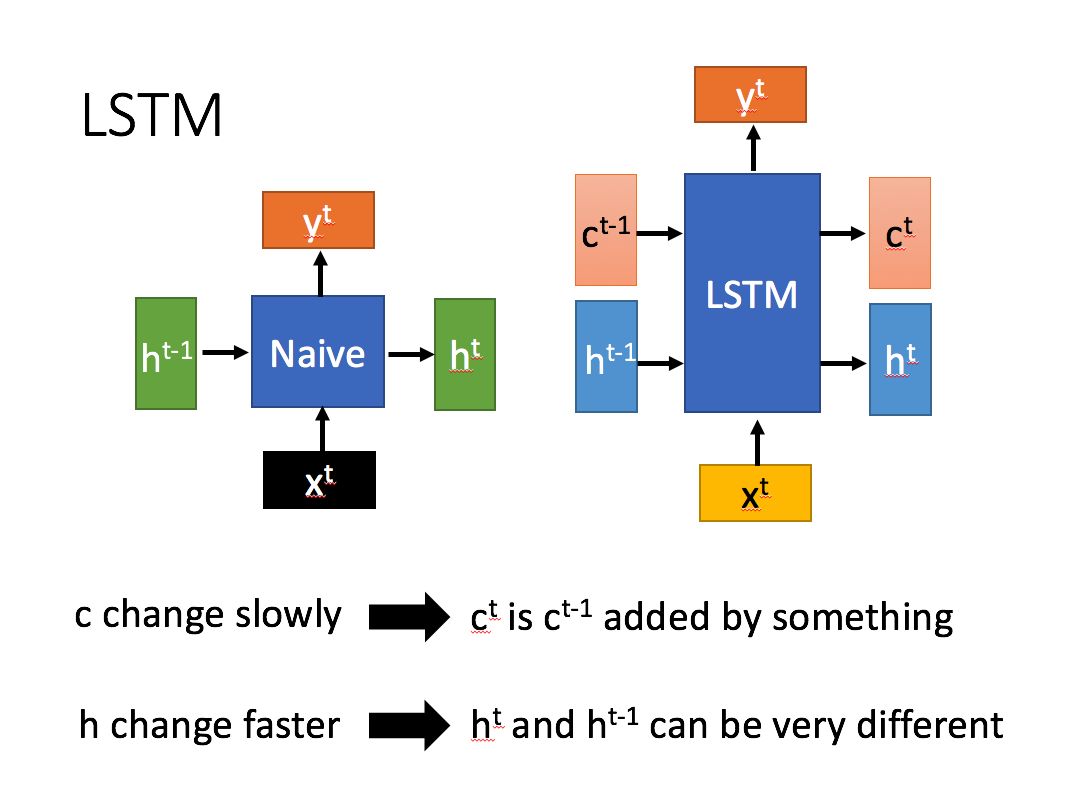
可以看到相比于RNN,LSTM有两个中间输出结果,并且其中c变化的比较慢而h变化的比较快,分别对应长短时信息(为什么会这样我们后面再说)。内部的具体结构则如下图所示,$\odot$ 表示元素对位乘,$\oplus$ 表示矩阵加法:
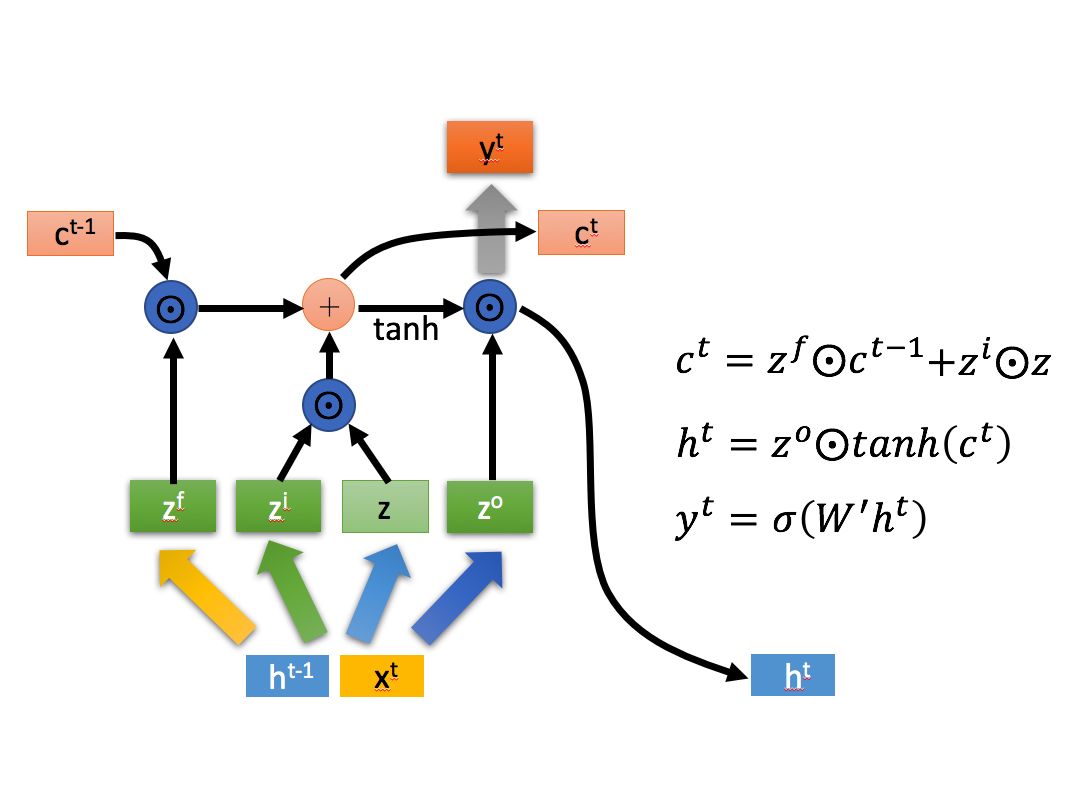
其中:
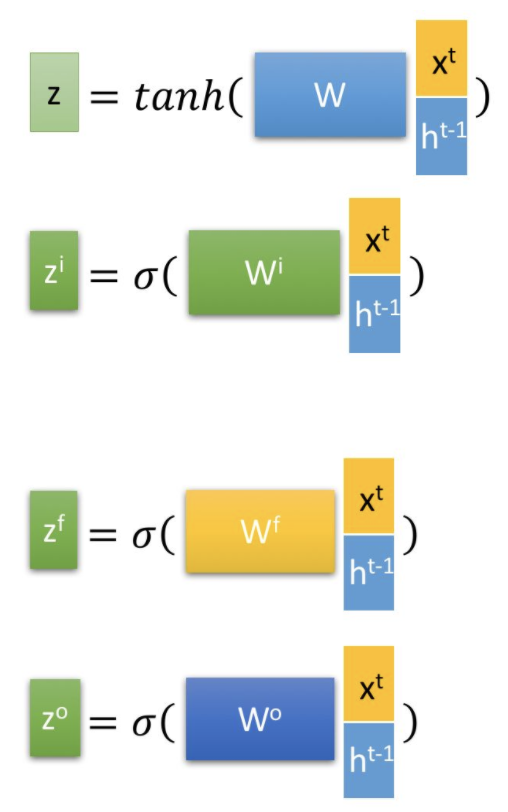
t时刻的x向量和t-1时刻的h向量拼接后经过四种不同的网络层,再经由激活函数得到四种不同的中间状态。其中后面三个由于经过sigmoid后会被映射到0-1之间(向量长度不变),因此可以看成是三个门控,来控制信息的流出。三个门从左到右(看第二张结构图)分别是忘记门、输入门和输出门,这几个门和z一起组成了LSTM的三个阶段:遗忘、加强和输出。
第一个阶段是遗忘阶段,其主体是忘记门。忘记门是第一个和t-1时刻的c状态发生交互的门,其作用是让t-1时刻的c状态被选择性遗忘,可以理解为进行了一次过滤。由于$\textbf{z}^f$的每个元素都在0-1之间,并且会和c进行对位乘,因此相当于是对c向量中的每个元素进行了缩减,如果对位的$\textbf{z}^f$的元素为0,那么其实就是将这部分信息抹去,即所谓的遗忘。
第二个阶段是记忆阶段。可以看到在遗忘阶段后,其输出会和另一个信息流进行累加并得到当前时刻的c。由于是累加,因此这一步本质上是对某些信息进行加强,或者说对某些记忆进行加强。加强的信息由输入门进行控制,其输入则是z。这里面有一个值得思考的小问题:
加强信息能否通过一个多层神经网络得到?即与单层神经网络结果经过输入门后的效果一样。
这个问题看上去可以转化为:能否用多层神经网络表示对位乘法?那答案当然是可以的,因为对位乘法其实就是某处位置的参数不为零而其他位置的参数为零,相当于参数矩阵是一个对角矩阵。但是能学不代表容易学。事实上神经网络就不是很善于学习单位矩阵,否则深度肯定越深越好,也就不需要什么残差网络了。
OK,回到网络本身。第三个阶段是输出阶段。在t时刻的c状态经过tanh激活函数后与输出门发生作用,可以得到t时刻的隐藏层结果$\textbf{h}^t$,$\textbf{h}^t$进一步经过单层网络和sigmoid函数得到$\textbf{y}^t$(即t时刻的y输出)。
这里需要注意的是:t时刻的c状态与输出门无关,输出门仅影响t时刻的输出y和隐藏状态h。那么问题就来了:
为什么输出和h要受到输出门的影响,而c不用?或者说输出门的作用到底是什么?
这个问题没有标准答案,就我个人的理解输出门的作用是对输出进行调整,调整的方式通过学习得到,调整的内容是经过非线性变换后的$\textbf{c}^t$,本质上就是所谓的“长短时记忆”(因为它既包含长时间记忆又包含短时间记忆)。为什么要对输出进行调整?我觉得这其实类似于attention机制,其目的在于寻找记忆中对于当前时刻输出有用的信息。因为这个信息是累积量,而累积量本身最好不要过多针对当前时刻的输入进行改变(可能会丢失对于将来某个时刻比较重要的信息),所以更好的做法可能是针对某时刻的输入(这里还包括上一时刻的隐藏层输出)进行筛选或者调整,这也就是为什么我们需要输出层。
LSTM的优势
LSTM最大的优势就是相比RNN来说在各个应用场景上带来了比较大的效果提升。提升的原因通常被认为就是它富有开创性的长短时记忆的结构。除此之外,LSTM还解决了RNN的梯度消失和爆炸问题。RNN的梯度消失和爆炸问题主要是由于RNN的权值矩阵循环相乘导致的。RNN的循环结构会导致它需要反复乘上自己的权值矩阵,而相同函数的多次组合会导致极端的非线性行为。LSTM通过其自身复杂的结构可以很好的解决上述问题。
LSTM的缺点
LSTM最大的缺点就是“太复杂”,这导致的结果是参数过多,训练时间太长。针对LSTM的这一个问题,研究人员提出了GRU,即门控循环单元网络,汲取了LSTM精华的门控思想,而同时又将其网络结构进行简化和改进,不仅速度更快,在某些场景下效果也更好。我们将在下篇文章中对其原理进行介绍。
总结
总结一下,LSTM通过门控的方式很好地控制了长时间记忆和短时间记忆的比重,并且针对每个输入和上一时刻的隐藏层结果对信息的抽取进行进一步的调整。LSTM很好的解决了RNN的梯度消失和爆炸的问题,并且取得了非常不错的效果。不过由于其参数过多,训练较慢,人们在其基础上进一步进行修改,并得到了诸如GRU这样兼具性能和复杂度的模型。