写在开头:这个系列主要记录一下个人学习博弈论时接触到的一些知识点,和一些有意思的game与现象,整体上并不保证连贯性。
五个入门结论:从与同桌的第一次博弈开始
假设你和同桌的成绩是由下面这个游戏的结果来决定的:
假设每个人都有两种选择: $\alpha$ 和 $\beta$ ,且当你们都选择 $\alpha$ 时可以一起拿到成绩B-;当你选择 $\alpha$ 并且你的同桌选择 $\beta$ 时,你可以获得A,而你的同桌只能获得C(如果选择相反则成绩相反);如果你们都选择 $\beta$ ,则成绩都为B+。那么你会选择 $\alpha$ 还是 $\beta$ 呢?
上面的游戏可以用一个结果矩阵(Outcome Matrix)来表示:
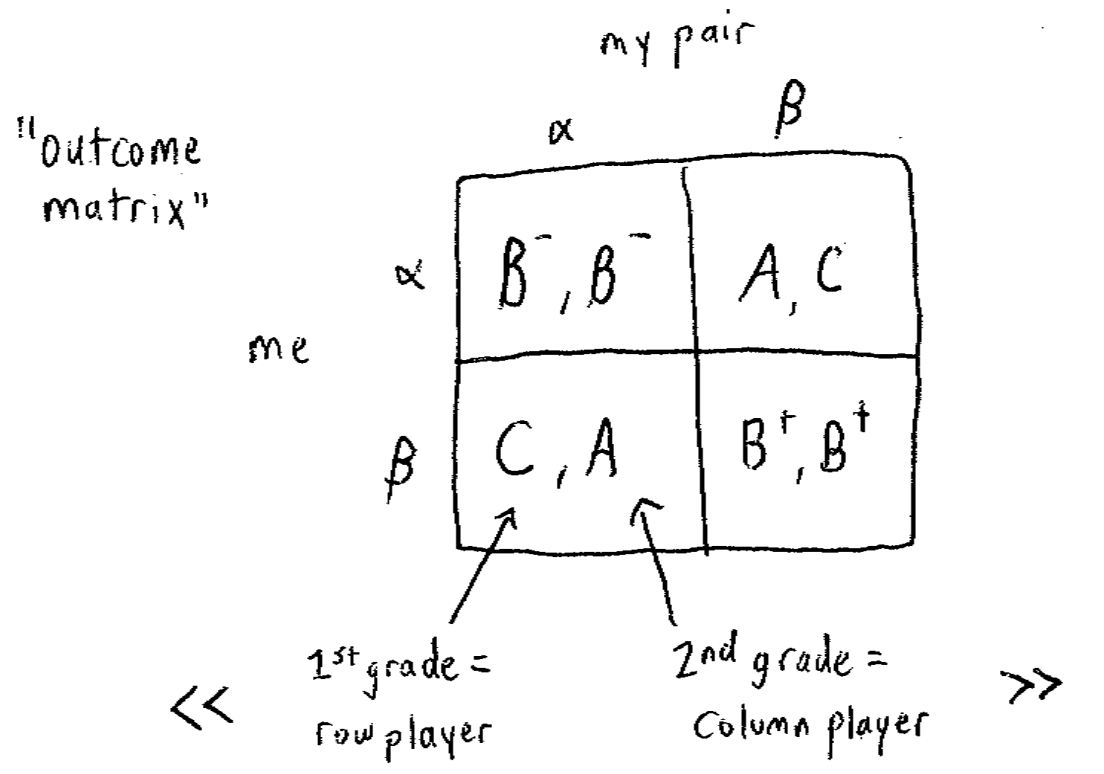
如果再将上面的成绩转换成数值:
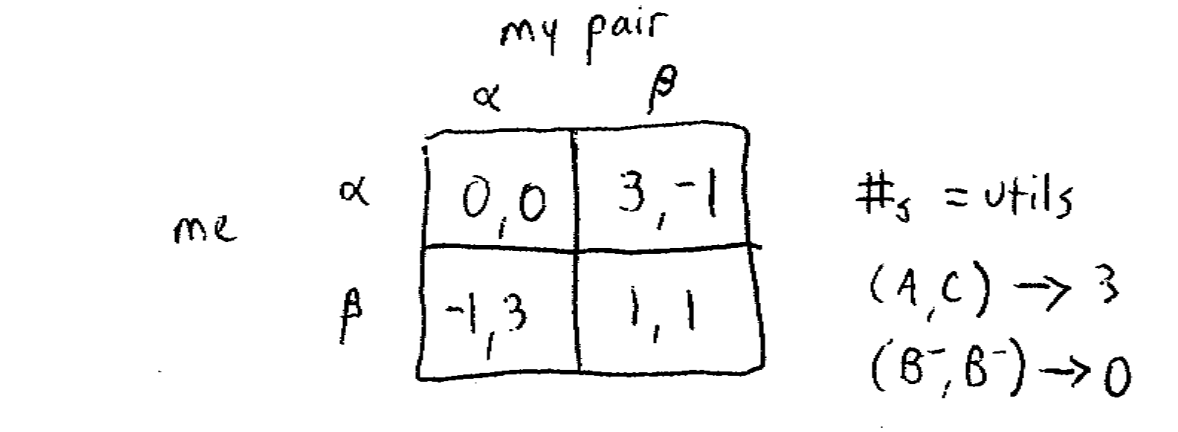
是不是看着清楚多了。那么这时你会选择 $\alpha$ 还是 $\beta$ 呢?
思考一下……
OK,公布答案:如果只为了自己的成绩考虑,那么你应该选择 $\alpha$ ,而不是 $\beta$ 。为什么呢?因为如果你选择 $\beta$ ,那么无论你的对手选择 $\alpha$ 还是 $\beta$ ,你的结果都不会比你选择 $\alpha$ 时更好,即所谓的strictly dominated。
定义:如果无论对方采用何种策略,策略 $\alpha$ 带给我的收益都严格大于策略 $\beta$ ,那么我们可以说策略 $\alpha$ 严格优势于(strictly dominates)策略 $\beta$ 。从另一个角度,我们也可以说策略 $\beta$ 严格劣势于(strictly dominated) 策略 $\alpha$ 。
两条定理:
- 定理一:不要采用严格劣势策略
- 定理二:理性的选择也可能会带来不太好的结果(如果大家都选 $\alpha$ 那么收益都是0)
假设有某种人(称为愤怒天使),他们会因为让别的了C而觉得愧疚,同时也会因为自己得了C而更加难过,则结果矩阵会发生改变:
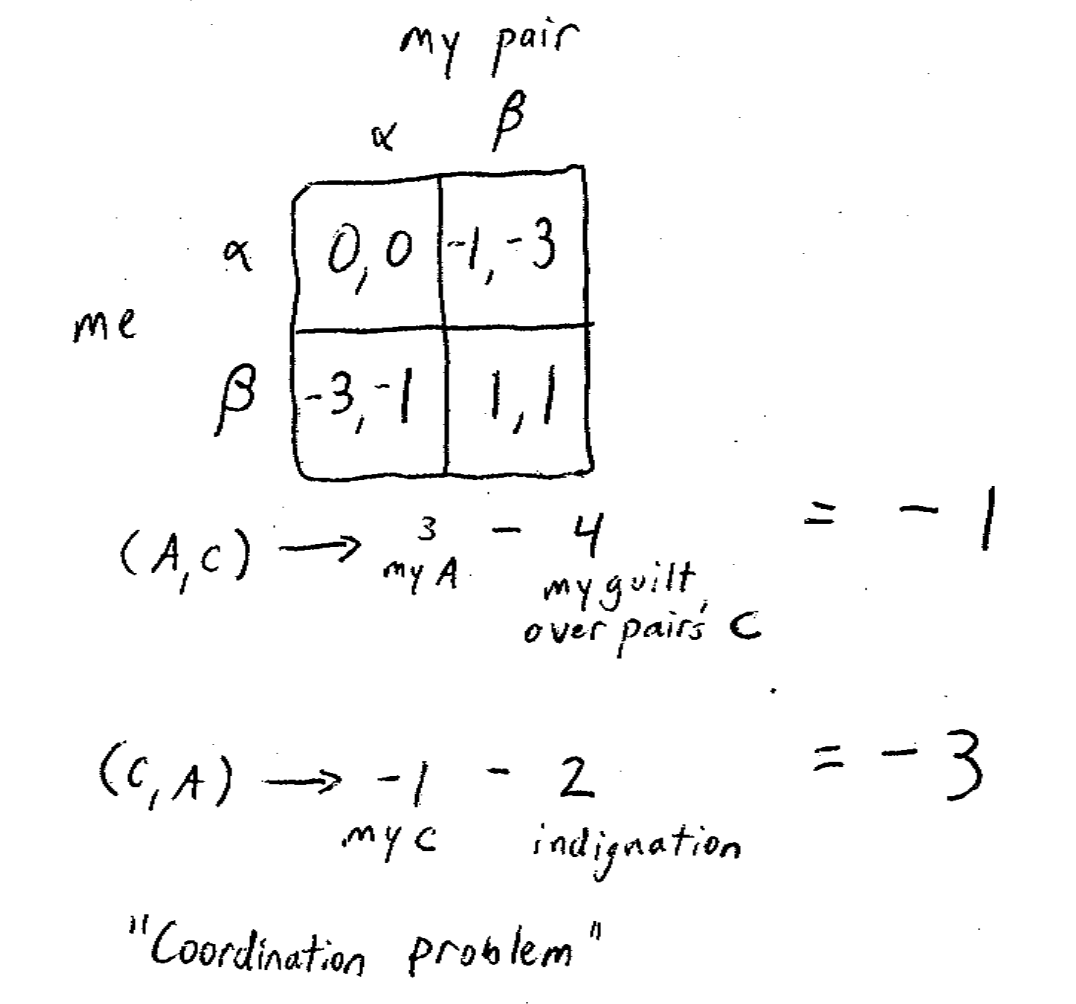
由此我们可以得到定理三:你只有先明白想要什么,才有可能得到它。
假设我们把拥有一开始的结果矩阵的人群叫饭桶恶魔(evil git),那么设想下面这个更复杂的博弈场景:如果你是一个饭桶恶魔,且你知道你的对手是愤怒天使,那么你该怎么做?
首先当然是画出结果矩阵:
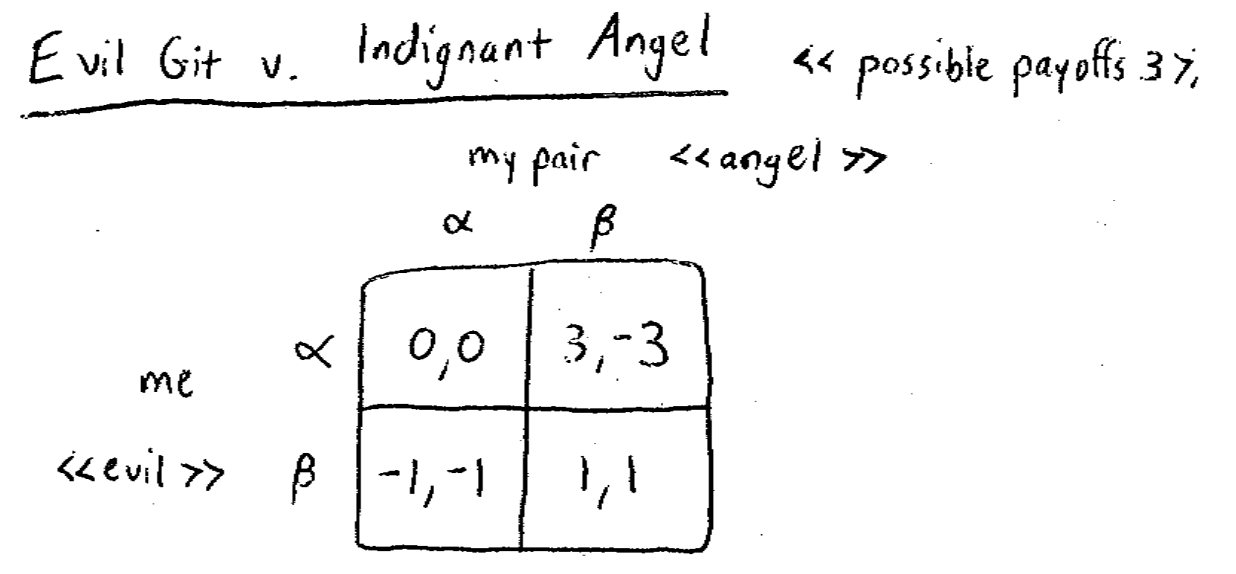
可见策略 $\alpha$ 依旧是严格优势策略。如果你们的角色对调,则结果矩阵为:
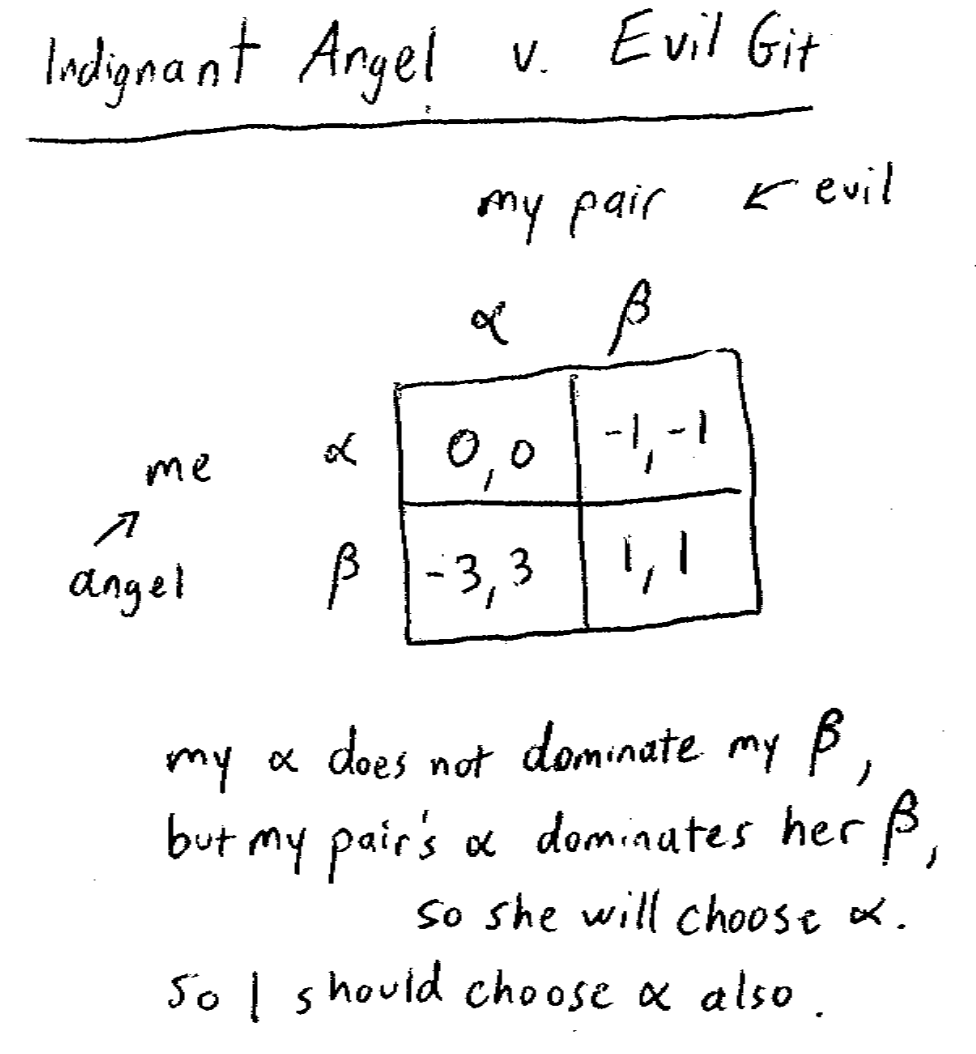
这时无论是 $\alpha$ 还是 $\beta$ 都不是严格优势策略。那是否你就可以选 $\beta$ 了呢?答案是否。因为对你的对手而言,策略 $\alpha$ 仍然是严格优势策略,因此我们需要假设对手会选择策略 $\alpha$ 。由此可以进一步得到定理四:学会换位思考,看看你的对手会做什么。
小结一下:
- 定理一:不要采用严格劣势策略
- 定理二:理性的选择也可能会带来不太好的结果(如果大家都选 $\alpha$ 那么收益都是0)
- 定理三:你只有先明白想要什么,才有可能得到它
- 定理四:学会换位思考,看看你的对手会做什么
学会换位思考
博弈中的几个要素
玩家(player):用符号 $i$ 或 $j$ 表示。
策略(strategy): $s_i$ 表示用户 $i$ 的一个策略; $S_i$ 表示用户 $i$ 所有可能的策略; $s$ 表示某次具体的博弈,我们也把它叫做一个策略组合(strategy profile),或者策略向量/列表。另外,我们把 $s_{-i}$ 看做是除了 $i$ 以外其他人的策略组合。
收益(payoffs): $u_{i}(s_1,…,s_i,…,s_N)$ 表示玩家 $i$ 在某个策略组合条件下的收益,因此也可以表示为 $u_i(s)$ ,或者 $u_i(s_i,s_{-i})$ 。
在之后的课程中会先假设以上三点对于所有人都是可知的,我们将在最后一节课推翻它。
数学化定义
之前提到的严格优势策略如果采用上面的符号可以表示为:
对于玩家 $i$ ,如果所有 $s_{-i}$ 都满足 $u_i(s_i,s_{-i}) > u_i(s’_i,s_{-i}) $,那么我们可以说的策略 $s’_{i}$ 严格优于 策略 $s_{i}$ 。
类似的,我们可以定义:玩家 $i$ 的策略 $s’_{i}$ 微弱优于(weakly dominates) 策略 $s_{i}$ ,如果对于所有 $s_{-i}$ 都满足 $u_i(s_i,s_{-i}) \ge u_i(s’_i,s_{-i})$ 并且对于某些 $s_{-i}$ 满足 $u_i(s_i,s_{-i}) > u_i(s’_i,s_{-i})$ 。
游戏时间
下面这个游戏可以很好地解释严格优势策略和换位思考的重要性。
假设每个人可以从1到100之间挑选任意一个整数作为答案提交,最终的获胜条件是尽可能接近所有提交结果的平均数的2/3,那么你会作何选择呢?
由于我们知道所有提交结果的平均数不会超过100,因此平均数的2/3也不会超过68。这意味着68-100之间的所有数字都是严格劣势策略,且不应被选择。剔除掉这些数之后,我们会进一步发现:当只能选择1-67时,比67的2/3 —— 也就是45大的数字也变成了严格劣势策略。如此不断迭代,最终的结果会趋近于1,即「正确答案」应该是1。
然而事实上,在耶鲁课堂测试中最后的获胜数字是9,而不是1。这就引出了一个重要概念 —— 共识(common knowledge)。尽管说所有人进行理性的结果会使获胜数字为1,但实际上一部分人并没有这么理性,而另一部分人并不确定有多少人的决策是理性的,也就是说博弈的玩家之间并没有形成共识。这里的共识指的是某个知识不仅被所有玩家认可,并且玩家之间也清楚对方也是认可的,同时玩家之间也清楚他们都各自清楚对方是认可的(无限套娃)。就好比说两个人各戴一顶帽子(假设都是粉色的),并且只能看到对方的帽子颜色而不知道自己的,那么此时“至少有一个人头戴粉色帽子”就不能算是两人的共识,因为他们只知道至少有一个人戴了粉色帽子,而不确定对方是否也知道。不得不说,这确实是一个很有意思的游戏。