拍卖机制的引入
通常情况下,不同的广告主对于某次曝光的价值认定是不同的,这不利于发布者形成对某次曝光的价值判断。在广告场景中,广告主和发布者双方需要一种公平且透明的方式来快速地得到一份针对某个曝光的合理成交价。拍卖机制就很合适。
拍卖通常分为三步:听取报价,选择报价,以及售卖给报价最高的人。在RTB中通常采用第二价格拍卖(second price auction)的方法,即最高报价者最终以第二高价格购买得到竞拍商品,且其他人都不清楚最终成交价。采用这种方式的原因是为了让价格更加稳定,这是因为如果直接以最高价成交,考虑到针对某个用户群体的曝光次数通常会比较多,那么广告主之间会互相试探对方,即从起拍价开始不断提高报价。又因为每个广告主心里都有一个最高承受价,一旦达到该成交价,其中一方就会放弃,而另一方由于缺乏竞争,可能会在之后将报价重新下降到起拍价,并在对手发现后重新开始试探的循环。
个人认为造成这一现象的主要原因是竞拍者在竞拍前明确知道自己以何种金额成交,而一旦改为第二价格拍卖,则用户会拥有更高的出价空间(因为最终成交价会低于自己的出价),并且倾向于出价更高(因为可能会占别人的便宜,同时也防止被别人占便宜)。可以说是一种很有意思的博弈过程造成的最终相对稳定的结果。
第二价格拍卖还有一个好处是会激励参与者展示他们自己心中认定的拍卖品价值(truth-telling),因为当其出价等于其所任务的拍卖品价值时,可以获取最高期望收益。之后作者在一个相对简化的场景下进行了证明。不过最后一段有点没搞懂,在b1 < v1时,为何b1等于v1的情况下期望最大,之后有机会可以请教一下作者。当然,在实际运用中会复杂很多,truth-telling也不一定是首要策略。
获胜的可能性
从统计学角度来看,假设一次曝光[2]由一个向量 $\mathscr{x}$ 来表示,并且服从分布 $p_x(\mathscr{x})$ ,那么针对某个策略下的报价 $b_{\mathscr{x}}$ ,最终能够获胜的报价分布 $q_x(\mathscr{x})$ 可以表示为:

即成功竞价的曝光分布等于某种竞价策略下的成功概率乘以曝光的原始分布。
由于我们采用第二价格拍卖方式,因此可以定义市场价格 $z$ 为某次拍卖中的第二高拍卖价格。假设其服从一种固定但尚未可知的分布 $p^{x}_{z}(z)$ ,那么以 $b_{x}$ 出价而取胜的概率为:
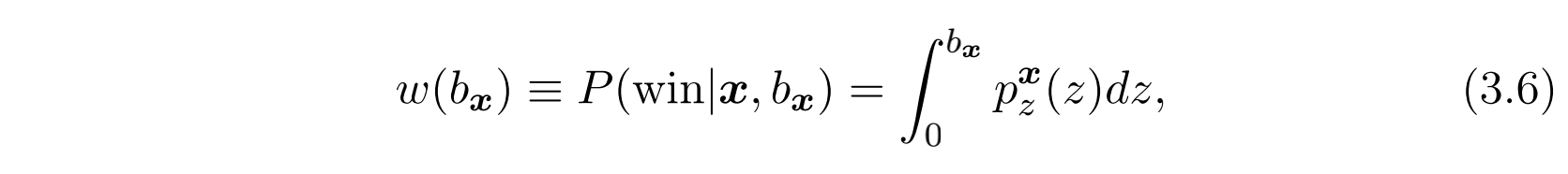
一般来说,为了降低估计的稀疏性,我们通常在campaign level而不是impression level去估计市场价格分布(也叫bid landscape),因此分布的表示也可以相应修改为 $p_{z}(z)$ 。
估计市场价格分布
承接上文,假设我们的报价是 $b$ ,那么赢得这次拍卖的概率可以表示为:
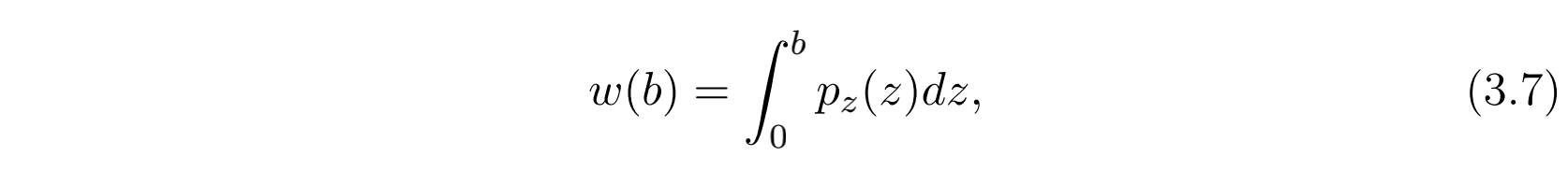
考虑到采用第二价格拍卖,则最终的期望花销是:
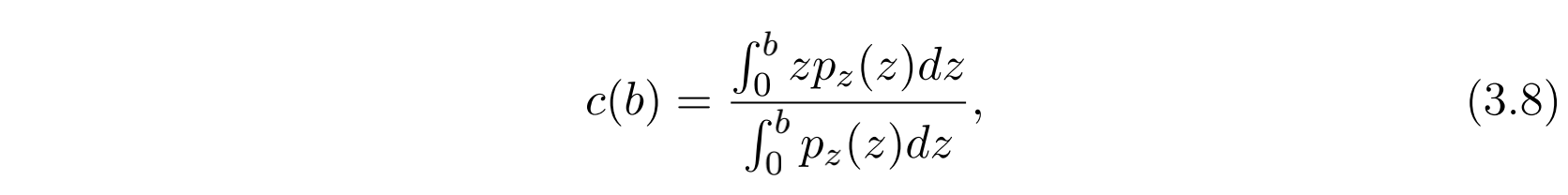
那么为了得到期望花销,关键是要估计 $p(z)$ 和 $w(b)$ 。下面介绍几种估计 $p(z)$ 的方法。
基于树的对数正态模型
这种方法[3]首先把campaign的目标规则切分成多个不相交的samples。每个sample对应于定向属性的一个独特组合,例如文中给出的例子 —— Gender=Male && Hour=18 && City=London。很显然,一个campaign下面可能有多个sample,即 $\mathrm{S}_{c} = {s}$ 。那为什么要将campaign拆分为多个sample呢?这其实是因为单个campaign的定向属性很可能随着时间而变化,并且面对一个新的campaign时,我们也很难预测。
对于每一个sample $s$ ,我们可以认为市场价格 $z$ 服从分布:
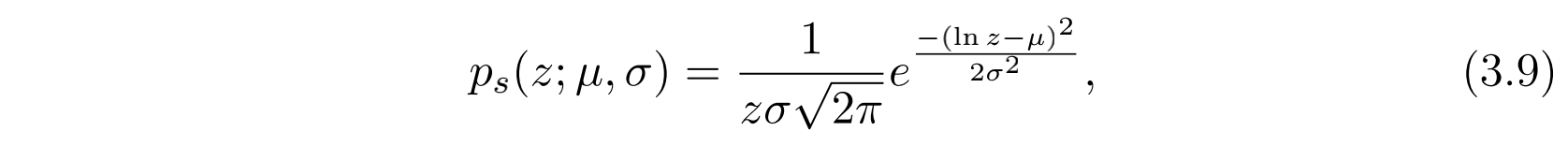
其中 $\mu$ 和 $\sigma$ 是对数正态分布的两个参数。那么下面的问题就是如何估计这两个参数了。作者采用GBDT来预测 $s$ 的期望和方差,并且根据下面的式子来转换得到对数正态分布的参数:
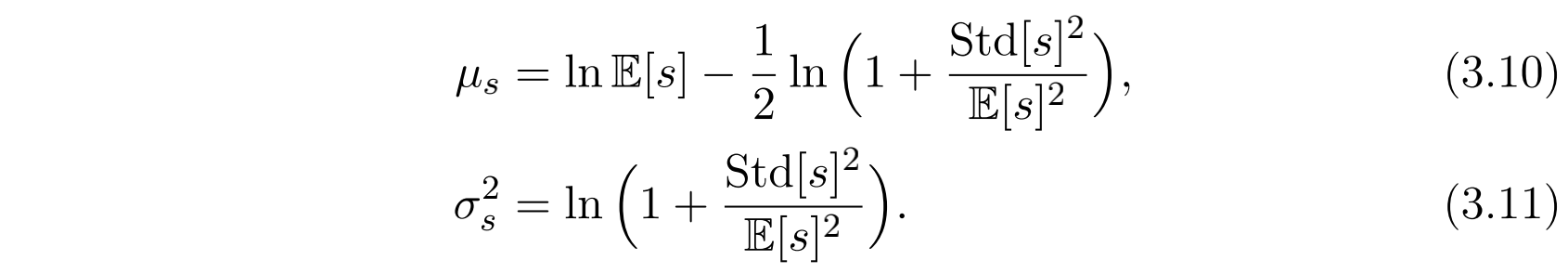
上面这个公式是由下面的对数正态分布的期望和标准差公式反推得到的( $D(x)$ 就是标准差的平方,期望和标准差的推导见知乎):
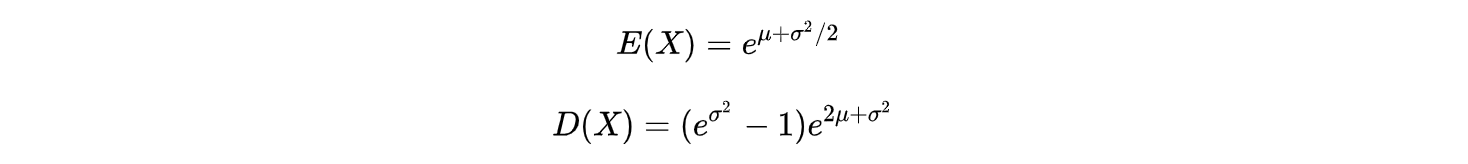
在得到 $p_s$ 后,campaign-level的获胜价格(或者说市场价格)分布可以表示为 $p_s$ 的加权和:
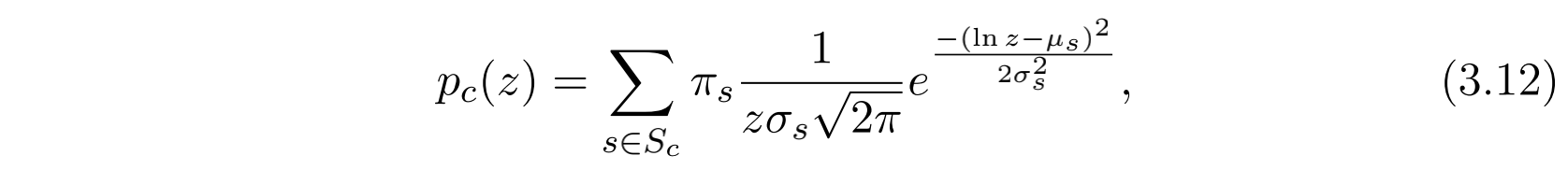
其中 $\pi_{s}$ 是sample $s$ 在 $S_c$ 中的先验概率(也就是权重),也可以定义为campaign的所有实例(曝光)中当前sample对应实例所占的比例(很明显和为1)。针对本方法的详细介绍我将放在附录A中进行介绍。
截断线性回归(Censored linear regression)
这种方法就直接很多,把 $z$ 的预测看成是一个回归任务,输入是竞价请求的特征向量。模型就是简单的线性回归,并且认为最终标签存在一个高斯白噪声:
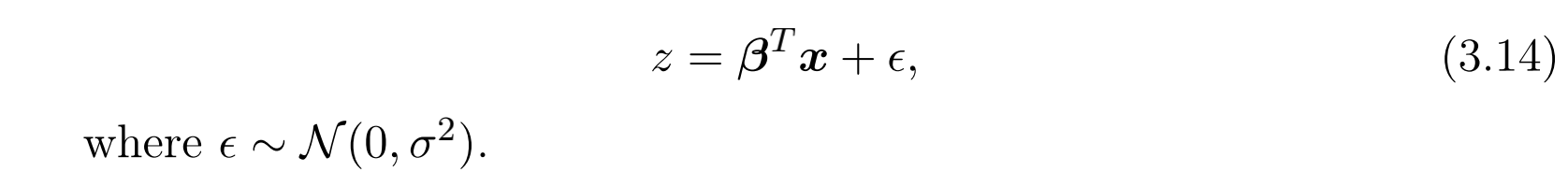
由于某个竞价只有在获胜时才能够被DSP得到获胜的价格,因此观测到的数据 $(\mathscr{x}, z)$ 其实是右截断(right-censored)的,也是有偏的(右截断是指只知道成交价格比出价高,而不知道具体值)。对于观测到的获胜价格 $(\mathscr{x}, z)$ ,其数据对数似然为:
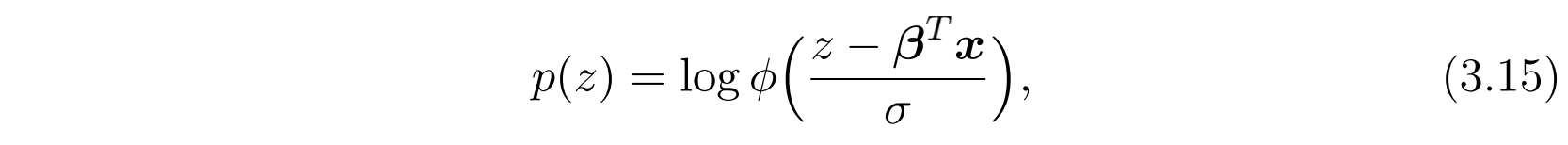
其中 $\phi$ 是标准正态分布的概率密度函数。对于失败的报价 $(\mathscr{x}, b)$ ,我们其实只知道最终价格是大于它的,因此部分数据对数似然(partial data log-likelihood)定义为预测的获胜出价高于该报价的概率,即:
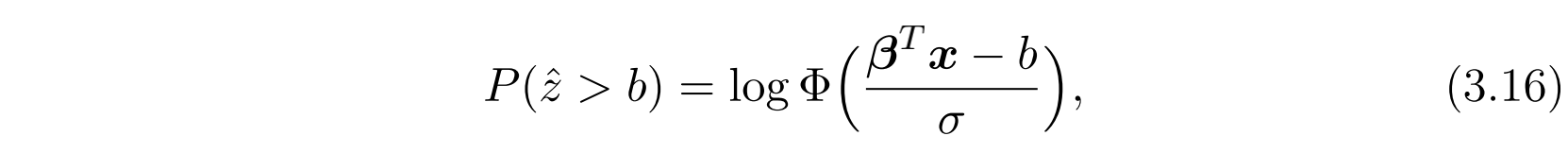
最后的目标函数其实就是:
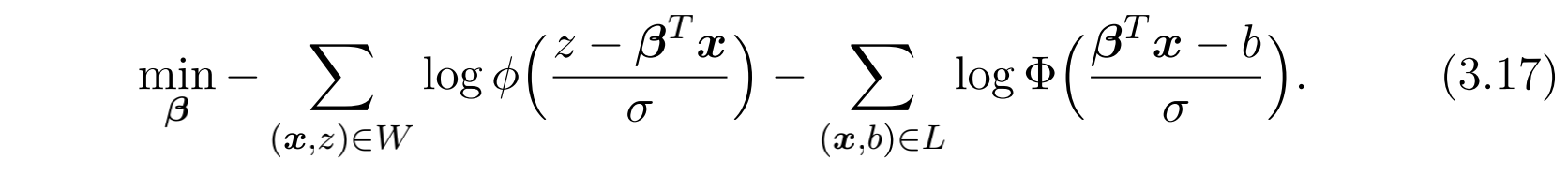
也就是说,对于竞价成功的实例,尽量让 $\mathcal{\beta}^{T}\mathscr{x}$ 拟合 $z$ ,而对于竞价失败的实例,尽量让 $\mathcal{\beta}^{T}\mathscr{x}$ 的值比 $z$ 大。不过我个人觉得这种方式不太靠谱,主要是因为后面这部分在第二价格拍卖的场景下远没有这么简单。
存活模型(Survival Model)
这里首先假设出价必须是整数。那么对于已经参加的 N 次RTB拍卖,我们可以得到 N 条拍卖结果,并以三元组形式展现: ${<b_{i}, w_{i}, z_{i}>}_{i=1…N}$ 。其中 $b_{i}$ 是第i次拍卖的出价, $w_{i}$ 是是否竞价成功的布尔值, $z_{i}$ 是竞价成功时对应的成交价。这些数据可以转化为另一种三元组形式: ${<b_j, d_j, n_j>}_{j=1…M}$。其中 $b_{j} < b_{j+1}$ (也就是说按照出价从小到大进行了排序,由于可能存在价格相同的出价,因此这里j的取值范围有了变动), $d_{j}$ 表示获胜出价正好是 $b_{j} - 1$ 的拍卖获胜次数, $n_{j}$ 表示以 $b_{j} - 1$ 出价无法获胜的拍卖次数。这里都已 $b_{j} - 1$ 为基准是因为我们采用的是第二价格拍卖,因此当我们出价为 $b_{j}$ 时就可以保证获胜 $d_{j}$ 次,而我们的实际出价是可能比这高的。由此可见,当我们出价为 $b_{j}$ 时,正好获胜的概率就是 $\frac{n_{j} - d_{j}}{n_{j}}$ 。那么对于出价 $b_{\mathscr{x}}$ ,输掉一场拍卖的概率为:
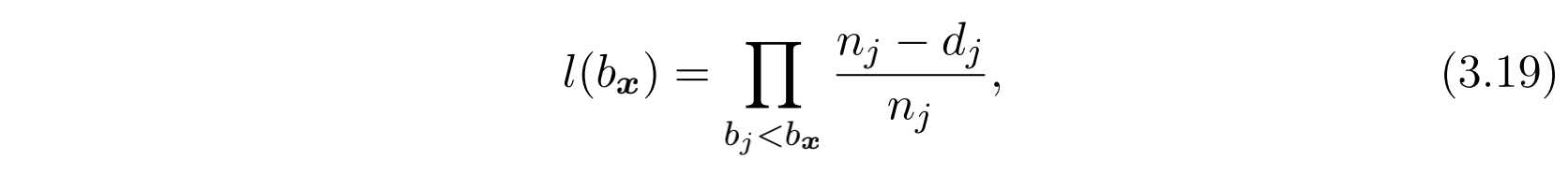
相应的,获胜的概率则可以表示为:
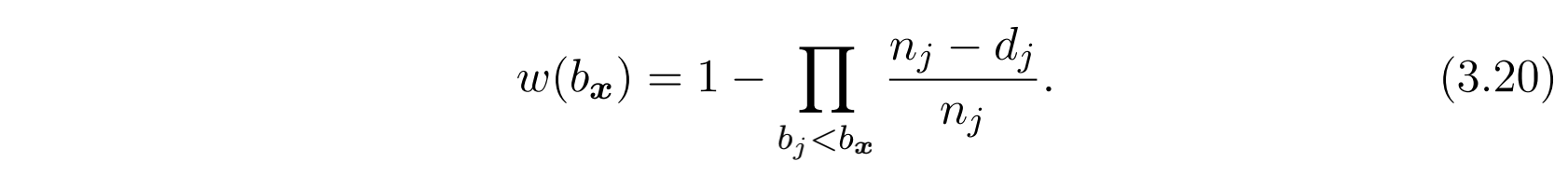
下图是一个示例:

其中 $w_{0}$ 是一个偏高的获胜概率估计,它假设所有的拍卖都获胜。示例还是很清晰的,这里就不多说了。上述的方法叫做Kaplan-Meier乘积极限法(Kaplan-Meier Product-Limit method),是一种无参的最大似然估计方法。
尽管市场价格分布预估是有价值的,但在实际应用中,频繁地重新运行线下的优化(采用实时数据更新landscape模型和竞价策略)往往更有效。这将在之后的文章中进行介绍。
附录
首先引用论文[3]中给出的一个例子来进一步形象化的解释campaign和sample的关系。假设一个campaign的投放目标是发布者P1和P2,并且是年龄在18-23或者30-35岁的男性用户,那么我们就可以将其拆分为多个sample来表示:
S1:publisher=P1,性别男,年龄18-23;S2:publisher=P2,性别男,年龄18-23;S3:publisher=P1,性别男,年龄30-35;S4:publisher=P2,性别男,年龄30-35。你会发现它其实就是所有可变属性的笛卡尔积。
对于上述4个sample,我们都可以用GBDT得到其对应的期望报价(estimated bid,相当于是预测过程)。其总体流程可以参照下图所示:
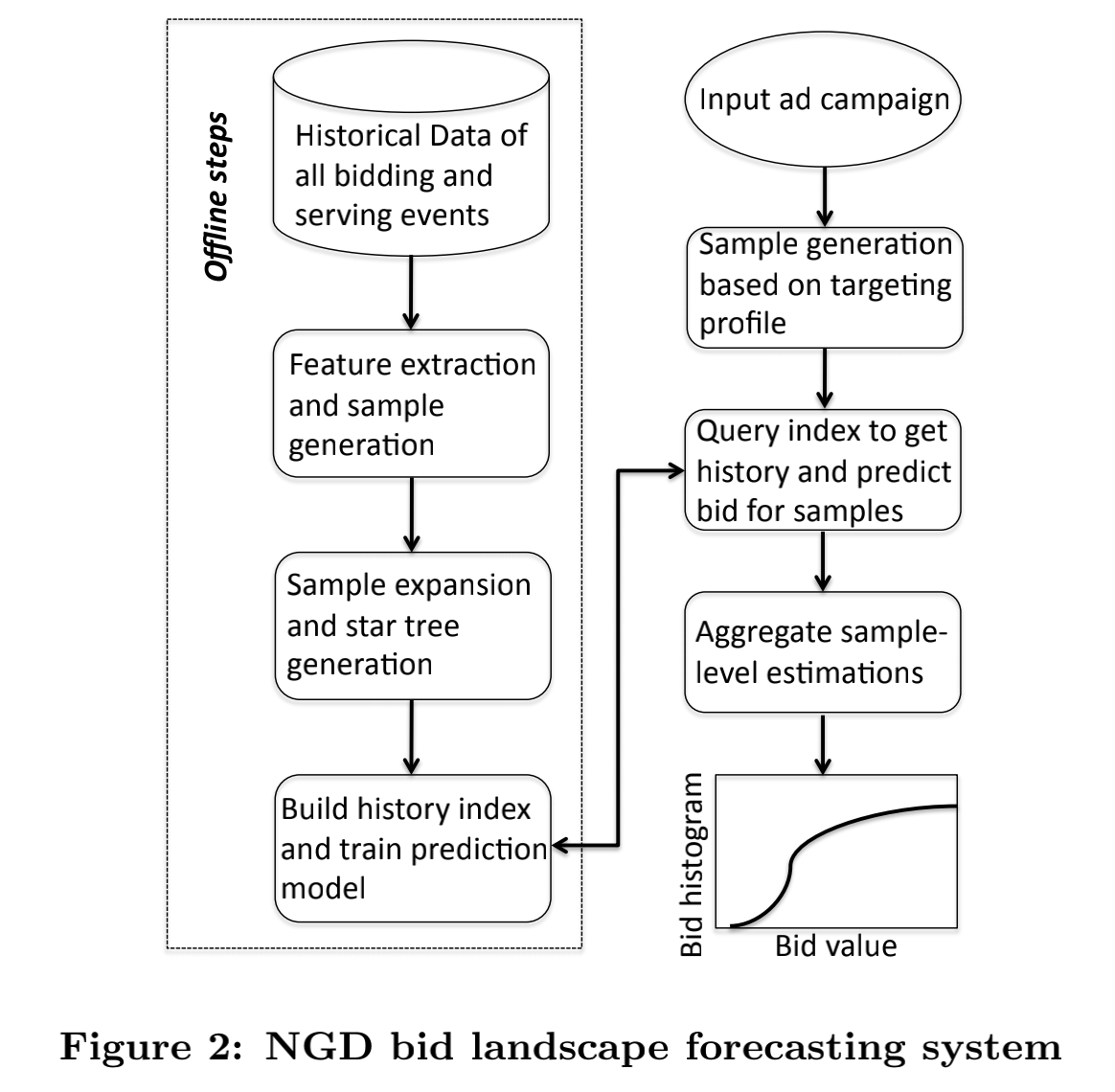
左侧是离线训练过程,大概分成四步:
- 数据采集
- 特征构建
- sample扩充和star tree生成
- 构建历史数据索引并进行训练
右侧则是在线预测的过程,大概分为三步:
- 基于定向档案的sample生成
- 依据索引获取历史数据,并进行预测
- 聚合得到sample-level的估计值
可以说整个过程还是很清晰的,下面再说说其中的一些细节部分。首先是离线训练部分:
采集的数据包括每一次竞价和服务事件(serving event)内的信息,具体有像广告机会、拍卖胜利者以及流量该曝光的用户等。每个广告机会都有很多属性,例如url、发布者、广告位置、用户人群、地理位置信息等。拍卖胜利者的信息则包括获胜报价的价格以及实际的支出等。由于特征数量特别庞大,因此作者采用了一种Fast-Correlation Based Filtering (FCBF)方法进行特征选择。
作者发现在NGD(non-guaranteed delivery)市场里,大多数sample的报价都是一个长尾分布,尽管大部分报价的价格比较低,但还是有不少数量的曝光机会获得了更高价值的报价。在对报价取log之后,其分布接近于正态分布,这也是为什么作者采用对数正态模型。我们知道对数正态分布由参数 $\mu$ 和 $\sigma$ 决定,而这两个参数又可以由期望和标准差反推,因此只要预测出期望和标准差,我们也就可以还原出原始的分布了。
由于预测一个sample的报价的期望和标准差需要它历史报价的期望和标准差数据,因此从工程上说需要一种手段可以快速获取任意定向属性值组合的历史报价数据。作者提出的方法是报价star tree扩充+通过模板进行历史查询(也就是上文中训练部分的第三步)。报价历史查找表可以被看做是一棵树,每一层对应于一个定向属性,而每个路径就是一个sample,如下图所示(其实就是笛卡尔积的树形式展示,还是很直观的):
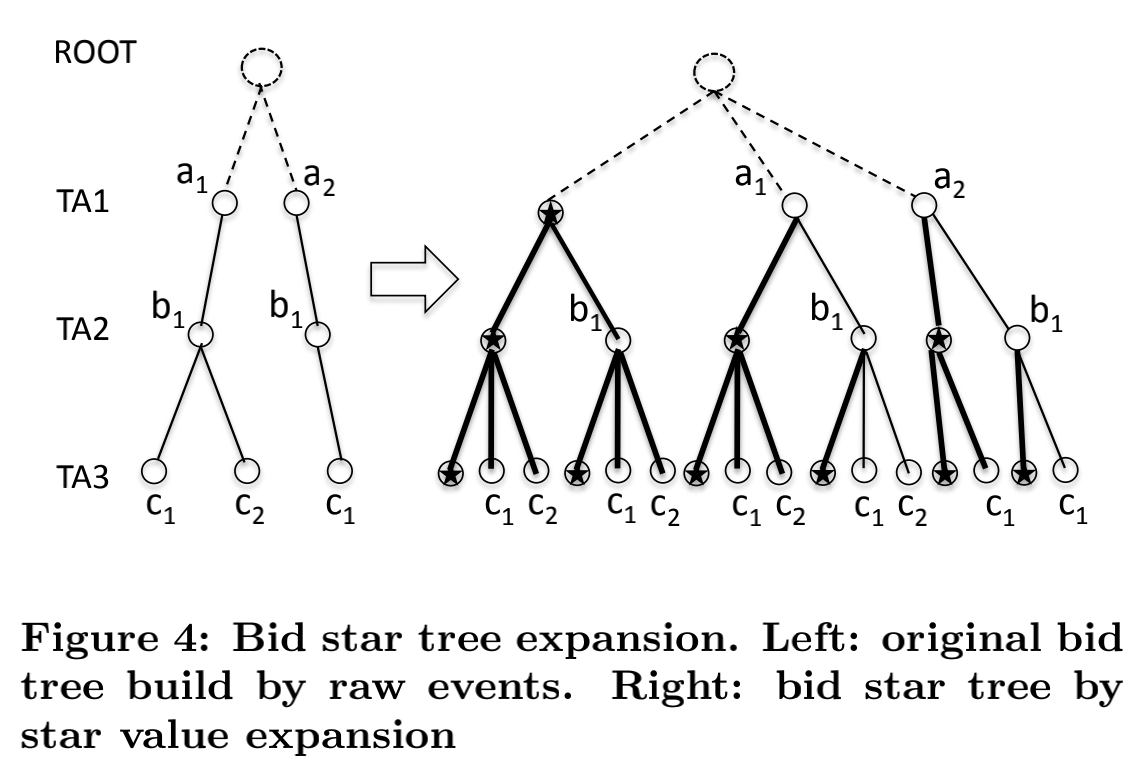
注意这里同一层的节点取值是有可能一样的,因为是树结构而不是类似于神经网络的结构,路径是不能交叉的。另外如果一个sample没有任何曝光历史,则不生成该路径(例如 $a_{2}b_{1}c_{2}$ )。具体的历史曝光会被assign到对应的叶子节点内。然而,这个简单的结构存在几个问题:
- 如果一个测试sample之前并没有观测到过(即没有对应的历史曝光数据),那么我们就没办法处理它。
- 很多sample的历史出价很少,其统计量不可靠。
- 从现实应用场景出发,某个广告主可能并不在乎某个属性的取值(即任意取值都可)。
因此我们需要引入一个平滑机制来处理未见过或者少见的sample,并且采取某种手段来满足第三点客户的需求。作者的做法是对于每个属性引入一个星值(star value)来表示“任意取值”。那么树的结构也就变为上图中右侧所示。引入星值后,每个曝光就有可能落入多个叶子节点中。对于之前提到的两个问题,如果没有历史曝光,那么可以以带有星值的路径来近似(例如 $a_{2}b_{1}*$ 或 $*b_{1}c_{2}$ );另外,对于那些曝光很少的路径我们可以直接删除,这样也节约了存储空间;当然第三个问题很显然也解决了,其对应的路径其实就是上图右侧树的最左侧路径。
当然,引入星值后也有一些“副作用”。首先就是一个sample对应的路径不唯一了。它所带来的结果就是我们需要一种方法去寻找和测试sample最接近的路径。这里接近是依据有多少相同数量的最重要的定向属性取值(是不是听上去还是很模糊,啥算重要?)来判断的。显然,没有星值的完全匹配路径肯定是最接近的。那么如果有星值呢?作者就引入了模板(template)的概念来解决这个问题。
一个模板被定义为一个针对每个定向属性的匹配类型组合。假如有D个定向属性,那么对应的模板都是D维的,其中每一个维度只有两个取值:完全匹配(被记为 $v$ )或者*。例如一个三维模板 $T_k = [v v *]$ 表示前两个属性必须完全匹配,而最后一个属性可以是任意的。如果给定一个需要进行搜寻的sample $s_i = a_{2}b_{1}c_{2}$ ,那么 ${s’}_{i} = a_{2}b_{1}*$ 就是其中的一个匹配结果。两者的相似度分数计算公式为各项维度的匹配值的加权求和,其中匹配值在两者完全相同时取1,否则取0,而权值则为特征重要性。我们知道模板的总数量是 $2^D$ ,这会引发维度灾难。其实也正是因为有这个问题,才引入了模板,因为可以对模板进行筛选。筛选的方式如下:
- 对每个模板算个质量分(确定值取1,星号取0后每个维度的加权和),并由大到小排序。
- 针对每个sample,取出当前质量分最高的模板,看是否匹配,如果不匹配就继续取,如果匹配就更新覆盖度评分(分数为当前sample所拥有的曝光量)并跳到下一次循环(也就是说一个sample只能给一个模板加分)。
- 依照覆盖度评分进行排序,由大到小选择TopK。
- 如果全星的模板未被选中,则最后再加上去。
考虑到质量分和具体sample和曝光都没有关系,可以离线先算好,并且针对每个sample更新模板覆盖度评分时一般前几个模板就能匹配上,所以总用时不算多(而且还可以并行化)。在预测阶段,假设我们之前选择了30个模板,那么会同时计算这30个模板和sample是否匹配,最终返回质量分最高的那个匹配的模板(这也就是为什么一定要有一个全星模板,否则可能匹配不上)。另外还需要注意,star tree的生成和模板的选择是采用不同时间段的训练数据完成的。
下面终于进入到模型训练部分了。这里训练的输入特征除了历史报价本身的特征之外还有用户侧特征以及发布者侧特征,类似于点击率预估里面除了点击本身的特征外也包括用户特征和物品特征。模型就是GBDT,任务类型是回归,目标值是某个sample的竞价期望和标准差。相当于是用现在的特征和经验分布去预测未来的分布。
在线预测部分我个人觉得还是比较直观的,因此这里就不再详细描述了。个人觉得这篇论文阅读文章写得也还不错,可以一起看看。
Reference
[1] Display Advertising with Real-Time Bidding (RTB) and Behavioural Targeting by Jun Wang, Weinan Zhang and Shuai Yuan. ArXiv 2016.
[2] 在文章中也叫bid request,个人认为应该是指请求别人(即广告主)进行竞价,其实直接理解为impression(曝光)可能更容易理解一些。
[3] Cui, Y., Zhang, R., Li, W., and Mao, J. (2011). Bid landscape forecasting in online ad exchange marketplace. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 265–273. ACM.