什么是实体对齐
简单来说,实体对齐就是将两个实际上表示同一个实体的不同样本对应起来,这两个样本一般位于不同的数据集内。实体对齐(entity alignment)也叫实体解析(entity resolution)、实体匹配(entity matching)或者记录链接( record linkage),其关键便在于如何关联两个样本。
实体对齐是一个应用广泛的概念,例如在知识图谱中也有相关应用。我们这里仅关注联邦学习中用到的一些实体对齐算法,暂时不进行更广的延伸。
为什么需要实体对齐
我们知道,在纵向联邦学习中,各个参与方的数据之间特征重合较少,而样本重合较多。那么如何确定重合的样本是什么?这就要用到实体对齐的技术。下面我们将以两篇纵向联邦学习论文中用到的实体对齐技术为例,展示其背后的技术原理。
纵向联邦中的实体对齐算法
纵向逻辑回归中用到的实体对齐
我们先来看一下这篇文章中用到的实体对齐方法。在无关隐私的场景下,实体对齐通常基于个人标识(personal identifiers)。例如名字、地址、性别以及出生日期等,这些都可以被有效利用的弱ID(weak ID)。这里作者采用了一种叫做cryptographic longterm key(CLK)的任意链接码(anonymous linking code)来进行实体对齐。CLK本质上是一个编码了多个个人身份标识的布隆过滤器(bloom filter)。
我们这里先简单解释一下布隆过滤器是什么。根据维基百科中的解释:
布隆过滤器实际上是一个很长的二进制向量和一系列随机映射函数。
布隆过滤器简单来说就是通过一系列的随机映射函数来将某组字符串(即一个集合)映射成对应的一系列很长的二进制向量,然后对这些向量进行与操作得到最后的代表这组字符串的二进制向量。当有一个新的字符串过来时,可以对它进行相同的映射以及与操作,然后再看它的二进制向量中取1的比特是否在集合对应的二进制向量同位置处也取1。如果是,说明该元素在该集合内,否则则认为其不在该集合。更详细的解释和相关证明可以参考这篇博客。
OK,说回CLK。上面说的编码指的是通过将选中身份标识的n-gram子字符串通过哈希方程映射到布隆过滤器的bit位置上来完成的。所以这里的布隆过滤器其实就是一种编码方式,利用了其空间效率和查询效率高的优点。此外,n-gram的作用更多是用于模糊匹配(即身份标识不必完全相同)。之后,对齐两个样本就可以转化为计算它们对应CLK的相似度。这里选用的相似度的计算方式是统计两个CLK编码bit的Dice系数。Dice系数的公式是:$ \frac{2 \times (A \cap B)}{A + B}$ ,其本质上和Jaccard系数差别不大。
下面是该算法中实体匹配的具体流程:
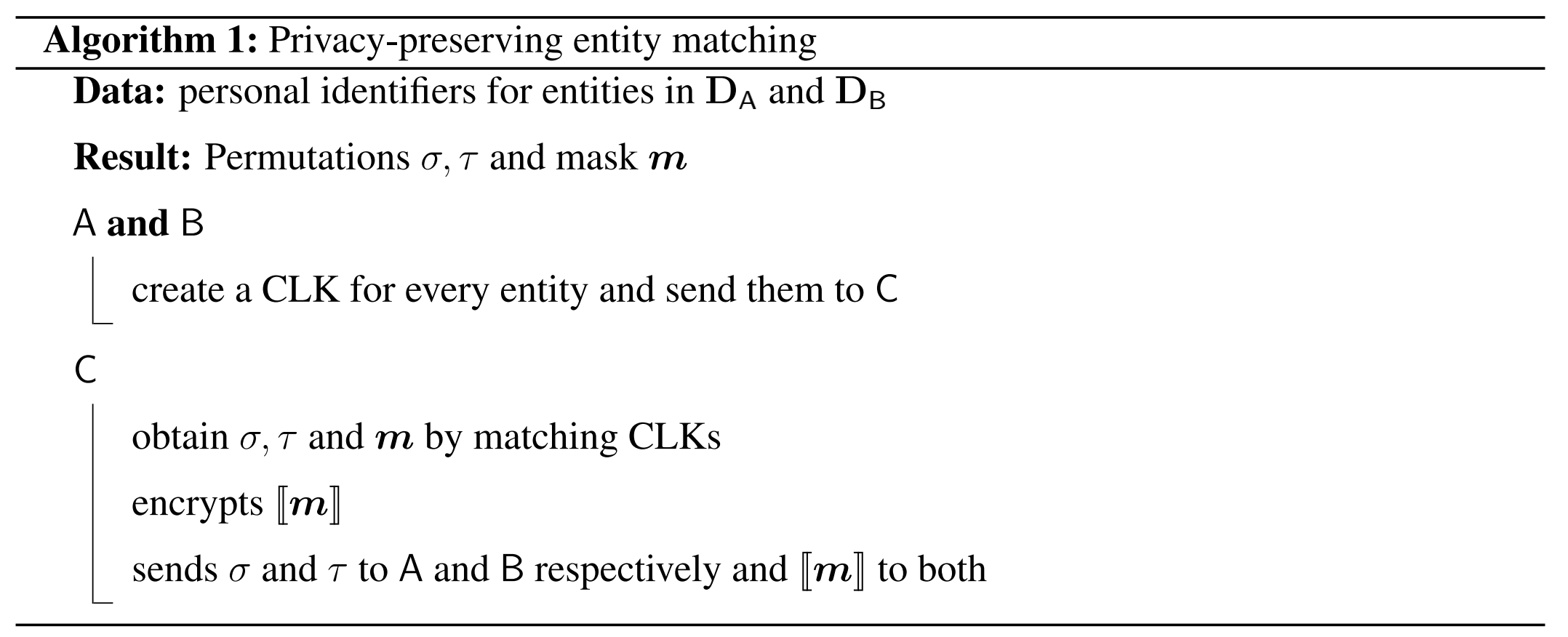
C处需要生成CLK两两之间的Dice系数,因此会得到一个大小为 $O(n_{1} \times n_{2})$ 的表,其中 $n_{1}$ 、 $n_{2}$ 分别是两个数据集的样本数量。这里只需要取最相似的pairs,所以可以用一种贪心的方式来进行。另外计算可以通过blocking来加速。
实体匹配的结果是两个排列 $ \sigma $ 和 $ \tau $ 以及一个伪装 $ m $ , $ \sigma $ 和 $ \tau $ 描述了A和B(这里假设两个参与方分别是A和B)需要如何重新排列他们的行来进行匹配(即一个统一的样本顺序),而 $ m $ 则表明某一行是否匹配上。
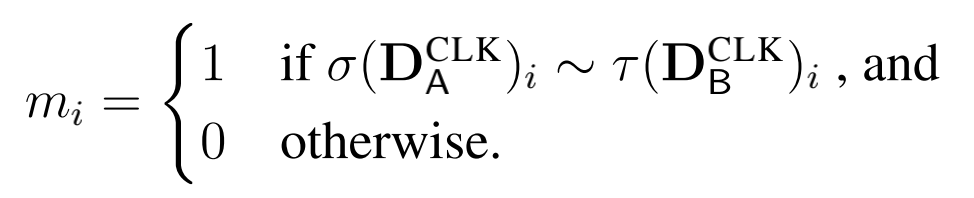
上式描述了 $ m $ 的取值,其中 $ D $ 表示数据集,~ 表示“很可能匹配上”。
这里对 $ m $ 进行加密(本文用的是Paillier同态加密)是为了防止参与方知道哪些人匹配上了。例如在医疗场景下,成功匹配实体可能表明不相关数据库中的人患有医疗疾病 ——
For example, when linking to a medical dataset of patients, successful matching of an entity could reveal that a person in an unrelated database suffers the medical condition.
不过我觉得这其实不是个大问题,因为没有标签的参与方并不清楚匹配上的人是否患病,而且在除医疗之外的场景下,这种加密就更显得鸡肋了。
最后总结一下,这种方法可以归结为:CLK + Dice系数 + 加密传输,本质上是用编码加相似度的方式进行快速以及模糊的匹配,虽然不能保证匹配上的样本就一定指向一个实体,但同时也相比于非常精确的匹配(即ID必须一样)提供了更灵活的空间。毕竟真实的数据很可能有着这样那样的问题,如何在这种情况下依旧可以匹配上实体也是一个比较困难的事情。
SecureBoost中用到的实体对齐
SecureBoost中用到的实体对齐方法与上面的有较大的差异,因为这里的匹配需要ID完全一致,而不是像上面那样支持模糊匹配。本方法来自Privacy-Preserving Inter-Database Operations[3]这篇文章,采用的是半诚实假设,并且目标是在匹配的同时不会泄露未匹配上的样本标记。
作者一开始提供了一些比较简单的思路。例如,可以使用普通的哈希比对,即同时对两个ID进行哈希操作,再比较其哈希值是否一样。但这个方法可能会受到domain attack,即攻击方知道样本domain(例如知道是身份证号码)的情况下,可以大大缩小他为了攻击而所需要进行尝试的范围,从而存在一定概率泄露原始信息。解决这一问题的方法是引入可信第三方来计算哈希值,或者通过SMC协议来避免隐私泄露。
另一种方法是使用AES03协议,它利用交换加密方案作为基石。交换加密方程 $f$ 具有以下性质:$ f_{a}(f_{b}(x)) = f_{b}(f_{a}(x)) $ .其中 $a$ 和 $b$ 是两个随机秘钥。具体的操作步骤见论文[3],这种方法感觉有点类似DH秘钥的生成方式,都进行了交换,只不过DH最后是保证两者的结果相同,原始的输入其实不重要,而这里则更关注原始的输入(因为最终对比的是输入)。此外,作者还引入了盲签名算法RSA来保证传输的主体没有被伪装。
这边先简单介绍一下盲签名。盲签名允许消息者先将消息盲化,而后让签名者对盲化的消息进行签名,最后消息拥有者对签字除去盲因子,得到签名者关于原消息的签名。盲签名就是接收者在不让签名者获取所签署消息具体内容的情况下所采取的一种特殊的数字签名技术,它除了满足一般的数字签名条件外,还必须满足下面的两条性质:
- 签名者对其所签署的消息是不可见的,即签名者不知道他所签署消息的具体内容。
- 签名消息不可追踪,即当签名消息被公布后,签名者无法知道这是他哪次的签署的。
上面的介绍摘选自百度百科,写的还是比较清楚的。我们下面举个例子来说明如何用RSA来做盲签名。假设 $e$ 和 $d$ 分别是RSA的公私钥,并且被参与方S拥有(即签名方是S)。首先由R选择一个随机数 $r$ ,并且发送 $x = m \times r^{e}$ 给参与方S(假设原消息是 $m$ )。S接收到之后返回一个签名过的结果 $x: sig’ = x^{d} = (m \times r^{e})^{d} = m^{d} \times r$ 。接着S再计算 $sig = sig’ / r = m^{d} \times r / r = m^{d}$,并将结果传给参与方R。这样一来,R便得到了签名者S关于原消息 $m$ 的签名。当然,上面的计算式将最后对N(即公钥)取模的操作都省略了,并且利用了RSA本身的一些数学性质,我们这里就不再给出具体的推导。
该方案最终的一个具体流程如下:
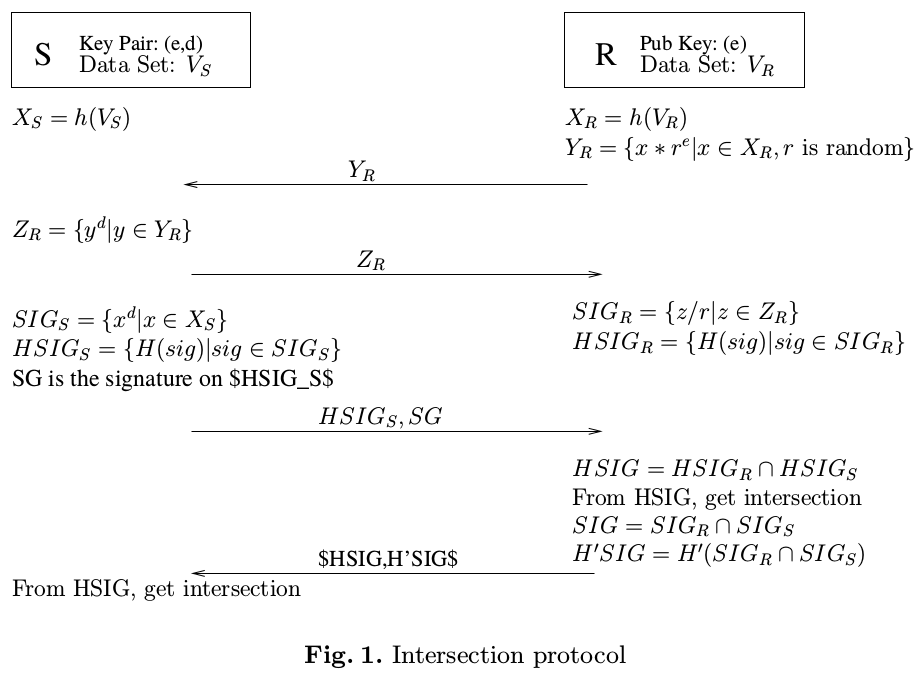
- S和R都在他们各自的数据集ID上应用一个哈希函数 $h$ ,它的作用是第一层防护。S会生成RSA的公钥和私钥,并将公钥 $e$ 发给R。
- R对本地哈希过的结果 $X_{R}$ 进行盲化,得到 $Y_{R} = {y = x \times r^{e} | x \in X_{R}}$ ,其中 $r$ 是一个对于每个 $x$ 都不同的随机数。
- R把 $Y_R$ 发送给S。
- S对 $Y_R$ 进行签名并得到签名结果 $Z_R$ ,再将 $Z_R$ 按照原顺序发回给R。
- R使用随机数r的集合来将集合 $Z_R$ 进行揭盲(unblind),并得到原消息的签名 $SIG_{R}$ .
- R之后再 $SIG_{R}$ 上运用另一个哈希方程H,并得到 $HSIG_{R} = H(SIG)$ 。
- S对 $X_{S}$ 进行签名后得到 $SIG_{S}$ 。之后同样将H运用于 $SIG_{S}$ ,得到 $HSIG_{S} = H(SIG_{S})$ 。
- S将 $HSIG_{S}$ 发给R,并对其进行签名得到SG,然后将SG也发给R,这样S就无法否认他将 $HSIG_{S}$ 发给了R。
- R对 $HSIG_{R}$ 和 $HSIG_{S}$ 进行比较,得到其共有的 $HSIG$ ,并由此得到SIG乃至真实的重合ID。
至此R方已经得到了最终的结果,但是S方还没有。在论文中,作者是通过R方将 $HSIG$ 发给S来让S获得两方的交集,而在联邦学习的开源框架FATE中,则是将上述过程进行了简化,并最终直接将交集发送给S。
总结一下,本方法通过多次哈希方程对原始结果进行加密,并采用盲签名来确保消息是被准确传递的。
小小的总结
上面的两个方法其实差别还蛮大的,这也说明联邦学习对这块的研究目前处于一个初期阶段,并且尚未形成一个共识性的有着良好效率和安全性的实体对齐方法。第一种方法的优势在于可以进行某种程度上的模糊匹配,而第二种的优势则在于计算结果并不存在假阳性的可能,整体的流程相对简单并且用到的RSA是比较常用的加密手段,工程上可以利用的现有轮子比较多,这可能也是FATE为什么采用第二种实体对齐方法的原因吧。
Reference
[1] Hardy S , Henecka W , Ivey-Law H , et al. Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption[J]. 2017.
[2] Cheng K , Fan T , Jin Y , et al. SecureBoost: A Lossless Federated Learning Framework[J]. arXiv, 2019.
[3] Liang G , Chawathe S S . Privacy-Preserving Inter-Database Operations[C]// 2nd Symposium on Intelligence and Security Informatics (ISI 2004). Springer Berlin Heidelberg, 2004.