论文简介
这两篇文章的本质都是在探寻一种将DNN运用于CTR领域的方式。由于CTR场景下特征多是离散类别特征,并且每个特征的取值个数不同,在经过One-hot后往往比较稀疏,所以并不适合直接接入DNN。一来参数量太大,二来特征过于稀疏,三来无法捕获特征间的local dependency。一个很自然的想法就是对原始特征进行一种通用的处理,然后将处理后的稠密特征输入DNN进行训练,得到更高阶的隐式交叉特征。FNN和PNN其实就是给出了两种对原始特征进行处理的方案。
FNN
FNN的想法很直观:
CTR场景 + 通用特征工程 + 生成稠密特征 = ?
FM!
FM似乎很适合来解决这个问题,因为它的隐向量就可以理解为是对原始特征的embedding。另外FM多用于CTR场景,也是一种通用的处理方式。由此,FNN应运而生:
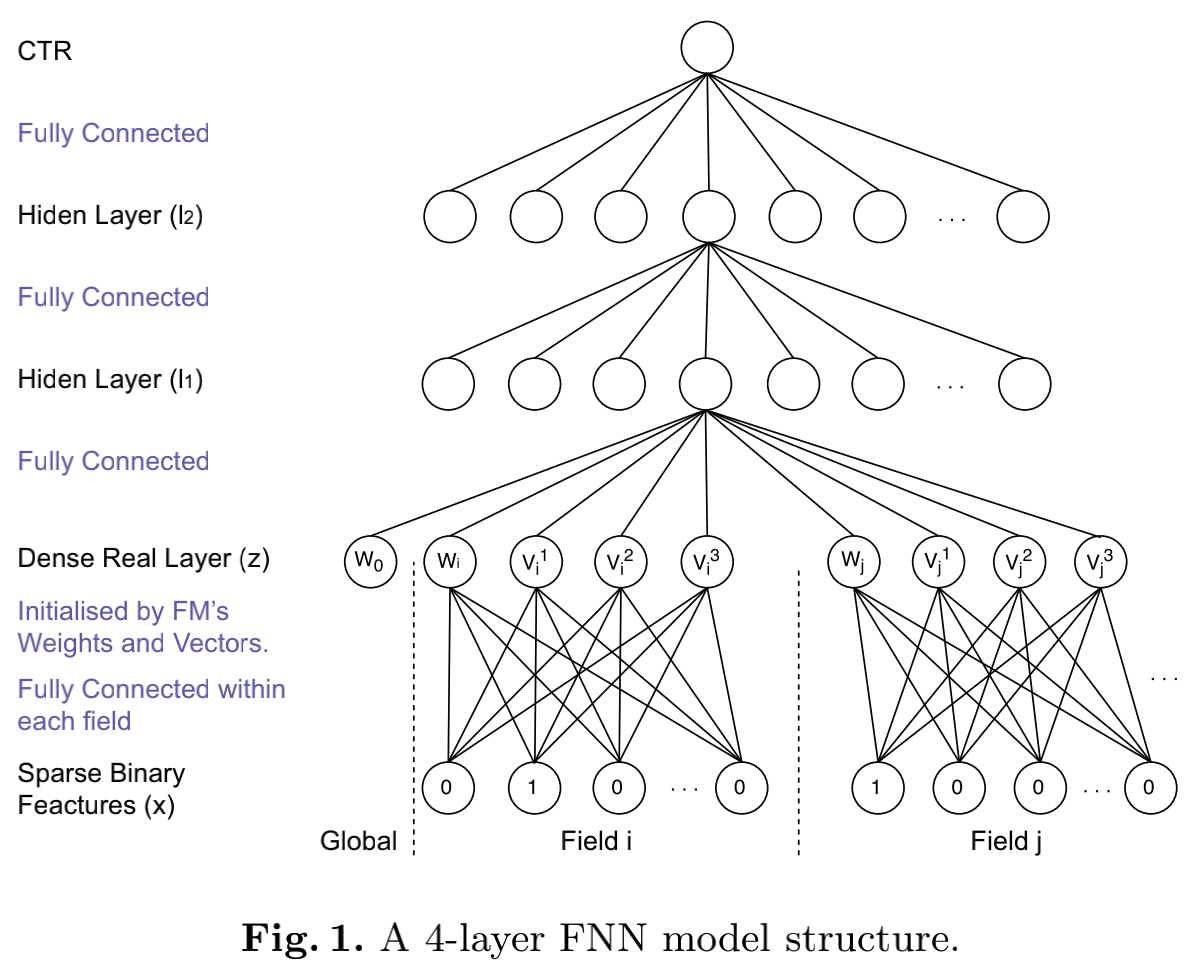
从上面的结构图也可以看出来,最上面几层就是典型的全连接层,而最核心的部分是最下面的稠密实数层(Dense Real Layer)。作者把原始稀疏特征划分为一个个field(和FFM一样),并针对每个field进行embedding。Embedding权重矩阵的初始值由各个【偏置+FM训练出来的隐向量】所组成。这篇文章中的某些公式个人感觉写的不是很不清楚,尤其是对于初学者来说。比如下面这个最关键的公式:
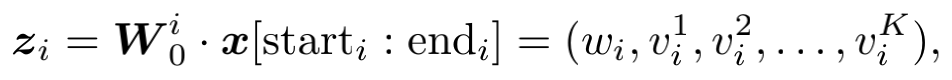
等式左边的z_i表示上面提到的稠密实数层中field i所对应的值(如果是初始值,那么其实就是FM的隐向量),而等式右边除了bias项外我们只得到了一个维度为K的隐向量,这看上去和FM中对每个field中的每个特征都对应于一个隐向量是不匹配的。不过事实上,这里的z_i或者v_i并不是一个“定值”。如果field i有m个特征,那么这里的vi1其实可以代表这m个隐向量中的任意一个的第一维度的值,具体等于哪个取决于输入的x在何处取1。也就是说,初始的权重矩阵Wi0其实就是[starti:endi]列隐向量,公式里的vi是依据x的取值对m个隐向量进行选择(选择取值为1的那一维度的隐向量)。
FNN给出了对原始特征进行处理的一种思路,但很显然,这其中存在两个问题:
- FM的训练和FNN的参数训练相互割裂。
- 在z到l1的映射中,embedding向量被拼接起来直接作为全连接层的输入,FM中的交叉特征并没有被显式地模拟出来。
前一个问题更多与工程应用相关,而第二个问题可能对模型效果影响更大,因为它本意是模拟FM,结果模拟到一半,在最重要的构建交叉特征的时候变卦了,改成由DNN自己构建隐式高阶特征了。针对上面提到的两个问题,PNN进行了相应的改进。
PNN
先看一下PNN的结构:
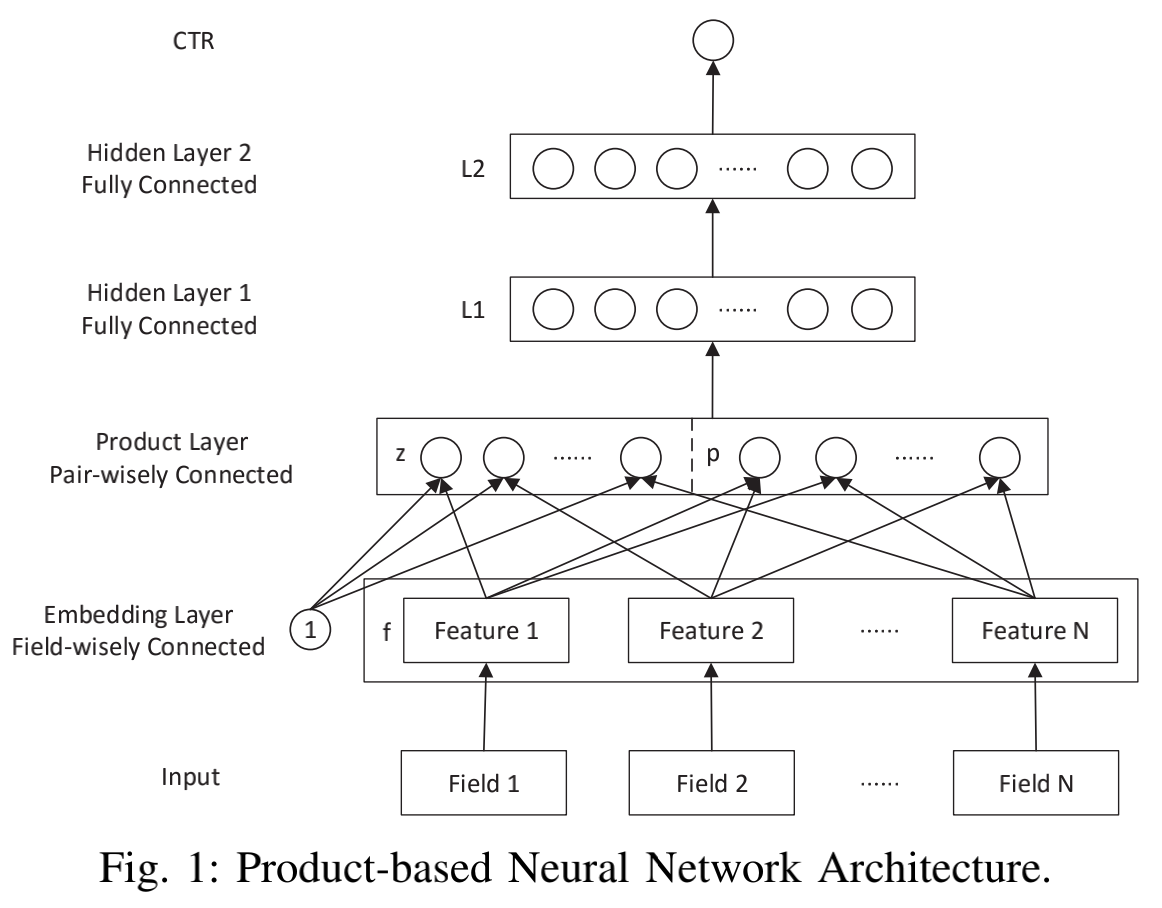
PNN中最关键的部分就是上面的Product Layer。这一层包括两部分,一部分输出直接对应输入(也就是上面的z),另一部分是两两特征之间做交叉(也就是p)。这里的特征对应于前面说的field,而交叉函数则可以自己给定。作者给出两种交叉方式IP(内积)和OP(外积),分别对应两种网络IPNN和OPNN。
IP其实就是对输入的两个向量做内积,也就是说上图中p后面的每一个圆圈就是一个内积后的标量值。而OP就是对两个向量做外积,那么p后面的每个圆圈就是一个M*M的矩阵。
得到p和z之后和权重矩阵进行对位乘法得到lz和lp向量:
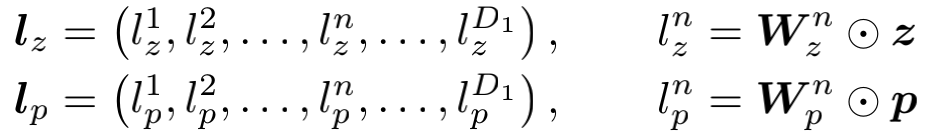
两者加上bias后经过relu便得到了l1的结果:
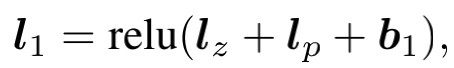
这两种方式都有对应的手段来减少时间和空间复杂度,这里就不细说了。对于上面提到的FNN的第一个问题,PNN的做法是通过上述的结构来直接模拟FM,而不是先训练一个FM,再用其隐向量来作为embedding。事实上,文章中也有提到PNN的product层本质上是FM的一种扩展:
if there is no hidden layer and the output layer is simply summing up with uniform weight, PNN is identical to FM.
另外PNN也是FNN的一种扩展,如果把lp那部分去掉,那么PNN就退化为FNN。
PNN带来的启发
PNN给人们如何处理CTR场景下的稀疏数据带来了启发,即可以通过embedding+product层的方式对稀疏数据进行降维,并模拟FM生成二阶交叉特征。DeepFM其实就是顺着这个思路往下延伸的。